Arithmethic - Geometric sequences

The two simplest sequences to work with are arithmetic and geometric sequences. An arithmetic sequence goes from one term to the next by always adding (or subtracting) the same value. For instance, 2, 5, 8, 11, 14,... and 7, 3, –1, –5,... are arithmetic, since you add 3 and subtract 4, respectively, at each step. A geometric sequence goes from one term to the next by always multiplying (or dividing) by the same value. So 1, 2, 4, 8, 16,... and 81, 27, 9, 3, 1, 1/3,... are geometric, since you multiply by2 and divide by 3, respectively, at each step.
The number added (or subtracted) at each stage of an arithmetic sequence is called the "common difference" d, because if you subtract (find the difference of) successive terms, you'll always get this common value. The number multiplied (or divided) at each stage of a geometric sequence is called the "common ratio" r, because if you divide (find the ratio of) successive terms, you'll always get this common value.

• Find the common difference and the next term of the following sequence:
3, 11, 19, 27, 35,...
To find the common difference, I have to subtract a pair of terms. It doesn't matter which pair I pick, as long as they're right next to each other:

11 – 3 = 8
19 – 11 = 8
27 – 19 = 8
35 – 27 = 8
The difference is always 8, so d = 8. Then the next term is 35 + 8 = 43.

• Find the common ratio and the seventh term of the following sequence:
2/9, 2/3, 2, 6, 18,...
To find the common ratio, I have to divide a pair of terms. It doesn't matter which pair I pick, as long as they're right next to each other:

The ratio is always 3, so r = 3. Then the sixth term is (18)(3) = 54 and the seventh term is(54)(3) = 162.

---

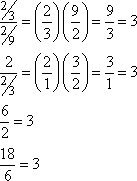
Since arithmetic and geometric sequences are so nice and regular, they have formulas.
For arithmetic sequences, the common difference is d, and the first term a₁ is often referred to simply as "a". Since you get the next term by adding the common difference, the value of a₂ is just a + d. The third term is a₃ = (a + d) + d = a + 2d. The fourth term is a₄ = (a + 2d) + d = a + 3d. Following this pattern, the n-th term a_n will have the form a_n = a + (n – 1)d.
For geometric sequences, the common ratio is r, and the first term a₁ is often referred to simply as"a". Since you get the next term by multiplying by the common ratio, the value of a₂ is just ar. The third term is a₃ = r(ar) = ar². The fourth term is a₄ = r(ar²) = ar³. Following this pattern, the n-th term a_n will have the form a_n = ar^{(n – 1)}.

• Find the tenth term and the n-th term of the following sequence:
1/2, 1, 2, 4, 8,...
The differences don't match: 2 – 1 = 1, but 4 – 2 = 2. So this isn't an arithmetic sequence. On the other hand, the ratios are the same: 2 ÷ 1 = 2, 4 ÷ 2 = 2, 8 ÷ 4 = 2. So this is a geometric sequence with common ratio r = 2 and a = 1/2. To find the tenth and n-th terms, I can just plug into the formula a_n = ar^{(n – 1)}:

a_n = (1/2) 2^n–1 
a₁₀ = (1/2) 2^10–1 = (1/2) 2⁹ = (1/2)(512) = 256

• Find the n-th term and the first three terms of the arithmetic sequence having a₆ = 5 andd = 3/2.
The n-th term of an arithmetic sequence is of the form a_n = a + (n – 1)d. In this case, that formula gives me a₆ = a + (6 – 1)(3/2) = 5. Solving this formula for the value of the first term of the sequence, I get a = –5/2. Then:

a₁ = –5/2, a₂ = –5/2 + 3/2 = –1, a₃ = –1 + 3/2 = 1/2,
and a_n = –5/2 + (n – 1)(3/2)

• Find the n-th term and the first three terms of the arithmetic sequence having a₄ = 93 anda₈ = 65.
Since a₄ and a₈ are four places apart, then I know from the definition of an arithmetic sequence that a₈ = a₄ + 4d. Using this, I can then solve for the common difference d:

65 = 93 + 4d 
–28 = 4d 
–7 = d
Also, I know that a₄ = a + (4 – 1)d, so, using the value I just found for d, I can find the value of the first term a:

93 = a + 3(–7) 
93 + 21 = a 
114 = a
Once I have the value of the first term and the value of the common difference, I can plug-n-chug to find the values of the first three terms and the general form of the n-th term:

a₁ = 114, a₂ = 114 – 7 = 107, a₃ = 107 – 7 = 100
a_n = 114 + (n – 1)(–7)

Suppose a1, a2, a3, …. is an A.P. and b1, b2, b3, …… is a G.P. Then the sequence a1b1, a2b2, …, anbn is said to be an arithmetic-geometric progression. An arithmetic-geometric progression is of the form ab, (a+d)br, (a + 2d)br2, (a + 3d)br3, ……

Its sum Sn to n terms is given by

Sn = ab + (a+d)br + (a+2d)br2 +……+ (a+(n–2)d)brn–2 + (a+(n–1)d)brn–1.

Multiply both sides by r, so that

rSn = abr+(a+d)br2+…+(a+(n–3)d)brn–2+(a+(n–2)d)brn–1+(a+(n–1)d)brn.

Subtracting we get

(1 – r)Sn = ab + dbr + dbr2 +…+ dbrn–2 + dbrn–1 – (a+(n–1)d)brn.

        = ab + dbr(1–rn–1)/(1–r) (a+(n–1)d)brn

        ⇒ Sn = ab/1–r + dbr(1–rn–1)/(1–r)2 – (a+(n–1)d)brn/1–r.

If –1 < r < 1, the sum of the infinite number of terms of the progression is

        limn→∞ Sn = ab/1–r + dbr/(1–r)2.